3.3.1. Expérimentation au collège Jean Dasté et dans la classe unique de Gumières

Au collège Jean Dasté, nous soumettions les élèves à trois termes : sondage, échantillon et statistique. Nous relevions que le mot statistique suscitait une évocation nettement moins fréquente que les deux autres et que l’étude en fonction de l'âge des élèves donnait les figures suivantes :

Figure 14 : Les termes sondage, échantillon et statistique selon les collégiens

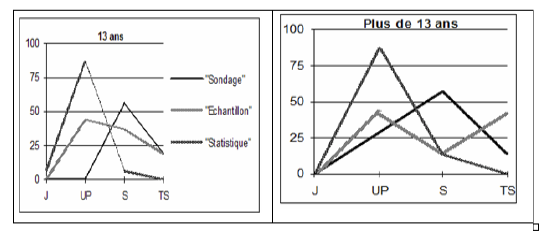
Apparaissait une stabilité des réponses des élèves (en fonction de l’âge et du sexe), qui laissait écrire alors : « La meilleure considération apportée au mot “échantillon” traduit certainement la sensibilité grandissante envers “l'échantillon publicitaire”! »  Soumis à différents items de prise de connaissance de ces termes, voici les réponses apportées par les élèves :

Figure 15 : Les apports de sondage, échantillon et statistique selon les collégiens

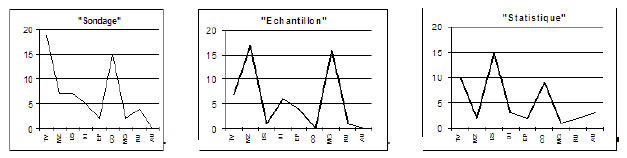
Ce qui nous permettait de conclure :

‘« Le mot échantillon a pour support, pour résonance spontanée les magazines et les magasins. Il évoque donc pour les élèves une image profondément et essentiellement médiatique. Statistique fait référence à livre scolaire et collège ; cette représentation demeure donc très scolaire. Quant à Sondage, il fait allusion à la télévision et dans une moindre mesure à collège. C'est donc un appel partagé aux domaines scolaire et médiatique. Comme on peut le constater, l'enseignement de la statistique ne pourra ignorer le support médiatique. Il devra également relier les espaces définis par les trois termes évoqués et harmoniser la confrontation des univers scolaires et extrascolaires. »’

Continuons dans cette approche, avec l’expérimentation conduite dans la classe unique de Gumières. A l’intérieur de cette classe unique, où nous étions l’enseignant, nous voulions tout d’abord percevoir quelles réponses donneraient des élèves de cycle III mis en situation d’incertitude (Annexe 5.2). Aux trois situations proposées :

• “- Sur 10 bébés qui viennent de naître, combien y a-t-il de filles et combien y a-t-il de garçons ?
• - Je prends un dé à jouer et je le lance 6 fois. Quels seront les six numéros qui vont apparaître ?
• - Dans un sac, je place 10 jetons jaunes et 10 jetons rouges. Si j’en tire dix, sans regarder, quelles seront les couleurs qui vont sortir ?”

Voici un exemple représentatif des réponses apportées par les élèves (Figure ci-dessous et Annexe 5.2) :

Figure 16 : Vers la création d’outils d’analyse statistique par les élèves.

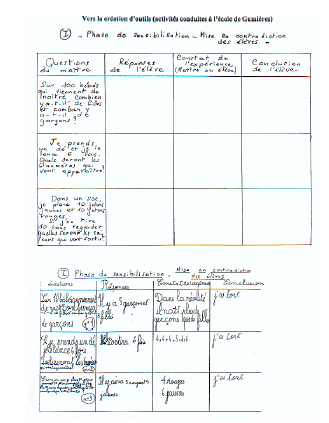
Ils étaient tous convaincus qu’un équilibre des réponses interviendrait dans tous les cas ! Ils sous-entendaient que le hasard installerait à notre insu une logique plus lointaine de régularité. Après même plusieurs essais, contredits par l’expérience, ils reformulaient le plus souvent une anticipation identique d’équilibre des résultats ! Ensuite, lorsque nous leur avons demandé d’utiliser un arbre de choix comme outil de simulation, l’utilisation en fut brouillée par le rapprochement avec les arbres généalogiques, les erreurs de construction et aussi par des choix qui donnaient priorité aux solutions régulières ou symétriques. Par exemple, une famille de 4 enfants se construisait selon eux, par ordre de préférence :

• soit 4 filles ou 4 garçons
• soit 2 filles + 2 garçons
• et après questionnement du maître : soit 3 filles + 1 garçon ou 1 fille + 3 garçons

Par contre la découverte d’une solution entraînait spontanément son symétrique.

Dans une phase suivante, nous voulions faire avec eux l’inventaire des supports graphiques de présentation de données au travers de revues mises à leur disposition. Très rapidement, ils listèrent et nommèrent à leur manière, différents modèles. Voici un exemple de réponses (Figure ci-dessous et Annexe 5.2) montrant que les élèves du cycle III établissaient une différence entre :

• d’une part, celles qui donnaient des résultats précis (idée de validité, de fiabilité dans le temps) et celles qui encadraient des résultats attendus entre des valeurs extrêmes ou par l’intermédiaire de % (le plus souvent, les premiers exprimés par des nombres et les seconds par des surfaces géométriques etc.)¹⁷.
• et d’autre part, celles que les élèves comprenaient et adoptaient par rapport à celles qu’ils rejetaient.

Figure 17 : Analyse par les élèves de leurs outils d’analyse statistique

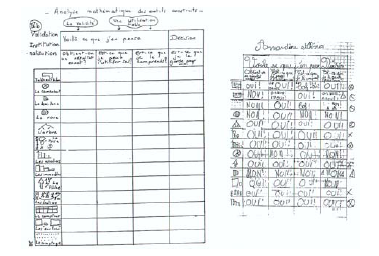
Les élèves semblaient pouvoir les utiliser seuls, mais, soumis à l’exigence de leur compréhension, ils maintenaient avant tout, ceux qui étaient construits à partir de données numériques¹⁸ . Les solutions gardées définitivement, mettaient en avant le tableau-bilan (habitude des exercices portant sur les factures), les arbres, les graphiques en bandes… et laissaient de côté les graphiques circulaires, demi-circulaires et rectangulaires. Nous percevions déjà là, une priorité scolaire qui marquait les réponses des élèves comme plus loin celles du maître ; priorité que nous retrouverons lors de la recherche de la partie 3 portant sur les choix des registres sémiotiques utilisés à l’intérieur des manuels de mathématiques du cycle III.

La phase n°4, de réinvestissement, devait faire prendre conscience aux élèves de deux éléments essentiels :

• la distinction entre les situations pour lesquelles nous pouvions envisager une réponse précise, mathématique, et celles pour lesquelles la réponse ne serait donnée qu’avec une certaine incertitude statistique,
• ainsi que la distinction entre une résolution appuyée sur une expérimentation (l’exemple du jet de dés), de celle basée sur une simulation modélisée (le profil d’une famille) comme le montre la réponse d’un élève de CE2.

Figure 18 : Expertise par les élèves de leurs outils d’analyse statistique

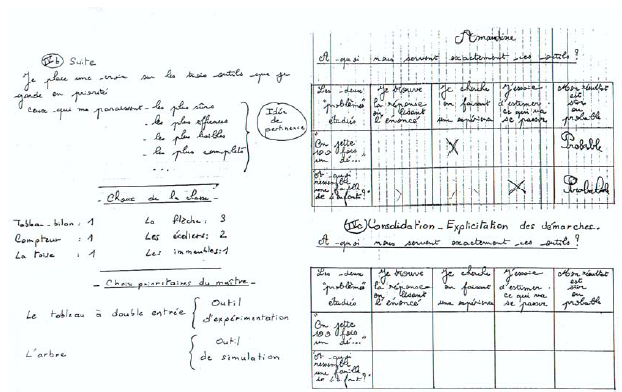
La phase suivante de complexification, montrait l’intérêt et l’efficacité qu’avait apportés ce travail. Nous ne relaterons ici qu’un seul exemple, celui qui demandait aux élèves d’anticiper leurs chances d’être interrogés par le maître en fonction de leur place respective dans la classe, face à lui, lors d’un regroupement (Annexe 5.3).

En conclusion, du côté des élèves, un travail devra être poursuivi pour redéfinir les notions statistiques utilisées, faire dépasser les faux à priori de régularité, équilibre, symétrie, qui imprègnent déjà les élèves de cet âge, élargir la gamme des représentations possibles et savoir choisir la plus adaptée, et enfin se positionner face à une situation statistique dont les données préexistent ou doivent être recueillies par l’élève au moyen d’une expérimentation ou d’une simulation. Passons maintenant à la deuxième phase de l’expérimentation au collège Jean Dasté.