Et ouverture au-delà de la conclusion

La question permanente, qui demeure au centre de la réflexion, est la suivante : comment aider les élèves à prendre une décision en situation incertaine ? Pour cela, nous pouvons observer le schéma suivant :

Figure 69 : Schéma de l’étude de la prise de décision par les élèves

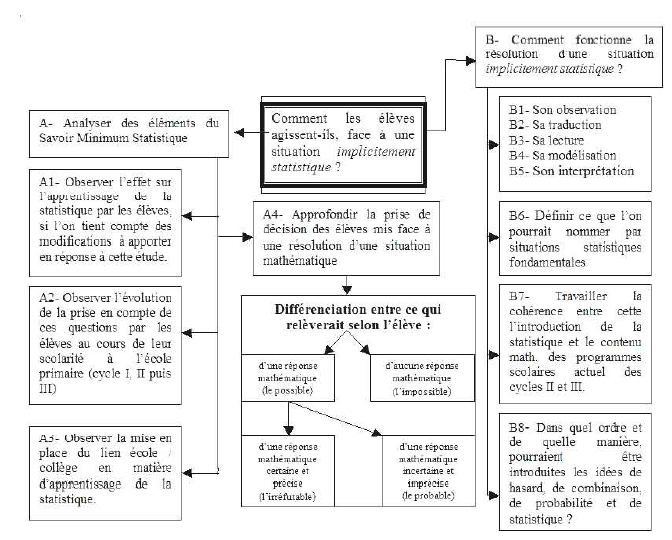
Deux types d’ouverture vers d’autres recherches, s’ouvrent donc ici.

Les premières, s’exerçant sur tout ou partie des éléments formant le contenu de ce que nous avons nommé le Savoir Minimum Statistique et les autres, portant sur des objets mathématiques plus généraux, non toujours spécifiques de la statistique comme la modélisation par exemple, mais interférant grandement dans son apprentissage par les élèves.

1-Des recherches s’exerçant sur tout ou partie des éléments formant le contenu du SMS

Plusieurs directions se dessinent pour rendre plus efficient, un enseignement de la statistique ; ce serait :

• pour A1 : d’observer l’effet sur l’apprentissage de la statistique par les élèves, si l’on tient compte des modifications à apporter en réponse à cette étude. Une première ouverture qui agirait de manière pragmatique par une prise en compte et un approfondissement des résultats obtenus lors des trois études précédentes portant sur les manuels scolaires,
• pour A2 : d’étudier dans les faits, l’évolution des représentations de la statistique par les élèves, et de leurs réponses aux situations dites implicitement statistiques, au cours de leur scolarité primaire : cycles I, II, et III (ceci en reprenant et complétant les critères élaborés au travers des expérimentations précédentes),
• pour A3 : d’analyser la mise en place possible, à l’écoute des professeurs du primaire et du secondaire, d’un apprentissage de la statistique dans l’idée d’un lien garanti entre l’école et le collège, et ensuite d’en observer l’efficience pratique auprès des élèves,
• pour A4 : d’approfondir la prise de décision des élèves mis face à une résolution mathématique au sens large, en la rangeant selon les trois entrées possibles :
• • là où selon l’analyse des élèves, le résultat existe, et pourrait donc être donné avec certitude et précision,
  • là où selon eux, le résultat est impossible à donner sur le plan mathématique,
  • là où selon eux, le résultat paraît incertain (l’entre-deux existant sur le plan mathématique, borné par les marges de l’impossible et du certain).

2-Des recherches portant sur des objets mathématiques, non spécifiques de la statistique comme la modélisation par exemple, mais interférant grandement dans son apprentissage par les élèves.

En ouverture évoquée à l’issue de la présentation à Bordeaux, nous avions avancé que l’apprentissage de la statistique ne pouvait se fonder : sans un retour sur l’analyse de la spécificité de la résolution d’une situation implicitement statistique. Il faudrait :

• pour B1 jusqu’à B5 : revenir naturellement sur les spécificités déjà repérées dans cette étude :
• • l’observation de la situation,
  • sa traduction,
  • sa lecture,
  • sa modélisation,
  • et son interprétation.

• pour B6 : essayer de définir ce que l’on pourrait nommer par situations statistiques fondamentales,
• pour B7 : en corollaire de l’ouverture précédente, étudier de façon plus poussée la cohérence entre cette introduction et le contenu mathématique des programmes scolaires actuel des cycles II et III,
• et enfin pour B8 : toujours en lien avec les ouvertures précédentes, analyser dans quel ordre et de quelle manière, pourraient être introduites les idées de hasard, de combinaison, de probabilité et de statistique.

Reprenons dans le détail, les quatre axes précédents :

• Retour sur B1 jusqu’à B5 :

Ces entrées pourraient prendre appui sur les réflexions de Jean-Claude Duperret (DUPERRET, 2001), et Jean-Claude Régnier (RÉGNIER, 2000), pour avancer le parti pris qui serait que, en lien avec les programmes actuels du collège, l’école devrait s’attacher à préparer les élèves du primaire à l’apprentissage de la statistique descriptive et plus particulièrement à les sensibiliser à l’idée de variabilité. Mais la variabilité doit se percevoir et s’étudier selon l’ensemble de toutes les étapes de la résolution d’une situation statistique :

Figure 70 : Reprise Figure 21: Représentation radiale de la résolution d’une situation statistique

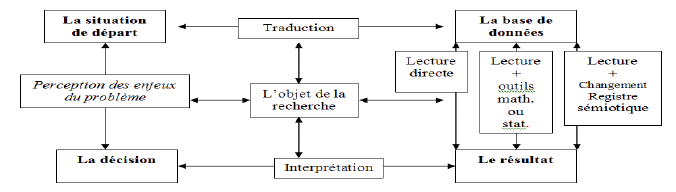
Des questions s’en détachent :

• L’observation : Comment lire notre environnement pour en percevoir des situations qui posent problème mais pour lesquelles se détachent une possibilité et une forme envisageable de traitement par la statistique ?
• La traduction : Comment repérer, choisir, “critérier” et mesurer les variables d’une situation relevant de la variabilité ? Comment choisir différents registres sémiotiques qui en permettront ensuite l’élaboration d’une lecture ?
• La lecture : Comment organiser une lecture en croisant les éléments précédents ?
• L’interprétation : Comment montrer alors aux élèves :
• qu’il ne faut pas confondre interprétation et subjectivité ! (Réflexion de Linda Gattuso Journées de la statistique de Lyon, 2003),
• que derrière tout cela, il y a des faits observables et que l’intérêt réside dans l’étude des liens qui se tissent entre eux,
• que le passage par des modèles mathématiques est indispensable pour aller vers une extension de la connaissance visible (projection dans le futur, élargissement et transposition des résultats pris sur un échantillon…) et pour aborder la lecture des diverses représentations (tableaux, graphiques…)
• La modélisation : Comment interpréter si l’on n’appuie pas cette situation sur un modèle mathématique ?
• Revenons sur B4 :

Comment sensibiliser les élèves à la modélisation ? Il paraît incontournable d’approcher l’interaction modélisation / concrétisation, sans retravailler, à partir des opérations arithmétiques déjà utilisées par eux à l’école primaire, l’idée de modélisation. Engager un va-et-vient permanent entre les trois aspects suivants :

• l’usage opératoire et la combinaison des opérations arithmétiques,
• l’utilisation de différentes représentations standardisées (registres sémiotiques),
• et enfin, l’illustration pratique des effets observés,

… permettrait-il une meilleure anticipation de la lecture de données statistiques et un meilleur traitement ? Est-ce que le fait de croiser les observations pratiques (par exemple des fûts de formes diverses à remplir…cf. situation proposée par les évaluations PISA), leurs traductions en opérations mathématiques et leurs représentations à partir de différents registres sémiotiques, permettrait une avancée notoire dans la capacité par les élèves à maîtriser ces situations statistiques ? Rappelons ici que dès 1989, nous pouvions lire :

‘« Il s’avère que lorsque les données du problème et les objets devant être utilisés pour sa résolution sont présentés sous forme figurative (graphique), les sujets réussissent un plus grand nombre de problèmes que lorsqu’ils sont soumis à une présentation verbale. On comprend bien que la présentation figurative (qu’elle soit concrète, graphique ou photographique) a pour effet de faire appréhender de façon directe par le sujet les propriétés des objets qui sont pertinentes pour le traitement du problème posé. »²³ ’

En un mot, comment faire comprendre aux élèves, que toutes nos traductions mathématiques, y compris celles réalisées à l’école primaire, ne sont souvent qu’une approche approximative des phénomènes observés dans la réalité ? Que l’usage des opérations arithmétiques scolaires de base (addition, soustraction, multiplication et division) ne reflète qu’une réalité idéalisée, épurée, pour permettre justement l’apprentissage de ces opérations ?

Comment dès lors, sans passer par cette nuance :

• d’une part, faire différencier l’usage de données statistiques de celui de l’outil statistique,
• et d’autre part, amener à faire anticiper à ce niveau d’enseignement, un prolongement de la description statistique d’une observation à la capacité d’élargir l’espace des connaissances de cette situation par l’emploi des probabilités ?
• Revenons sur B7 :

La troisième ouverture pourrait déjà essayer de répondre aux interrogations soulevées à l’intérieur de la présente étude. En particulier, pour ne pas risquer de limiter ultérieurement la découverte de la statistique, comment enseigner aux élèves, les éléments suivants :

• l’approche de la chaîne numérique,
• la découverte et l’usage des tableaux à double entrée,
• la pratique des comparaisons, et leur combinaison avec les transformations,
• la découverte des aspects qualitatifs, l’appréciation des données de rang,
• l’identification de la population analysée et son observation (enquête…)
• etc.

• Retour sur B8 :

Se poser la question de l’ordre et de la manière, avec lesquels pourraient être introduites les idées de hasard, de combinaison, de probabilité et de statistique, nous reconduit à deux documents que nous avions déjà mis en avant lors de nos précédents écrits (COUTANSON, 2004) : un ouvrage intitulé : Combinatoire, statistique et probabilité de 6 à 14 ans, (VARGA T., DUMONT M., 1973) ainsi que la publication d’une expérimentation conduite auprès d’élèves suisses (document disparu dans l’incendie de la Bibliothèque de LYON 2 et donc difficile actuellement à “réidentifier”). Les deux premiers auteurs, préconisaient une logique d’apprentissage de l’incertain passant successivement par la combinatoire, les probabilités et les statistiques. De son côté, le document suisse évoqué, se fondait sur l’échelonnement des périodes d’appropriation cognitives de l’enfant (PIAGET J., INHELDER B., 1951), présenté de la manière suivante :

Tableau 99 : Évolution des formes de résolution de problèmes par les élèves en fonction de leur âge

	Opérations logiques	Idée de hasard et de probabilité
Première période (7/8 ans)	Absence d’opérations proprement dites (niveau préopératoire)	Indifférenciation du possible et du nécessaire, du déductible et du non déductible
Deuxième période (8/11 ans)	Construction de groupements opératoires d’ordre logique (niveau des opérations concrètes)	Différenciation et antithèse entre opérations (domaine du déductible) et hasard (domaine de l’“incomposable” et de l’irréversible)
Troisième période (11/12 ans)	Opérations au niveau formel	Synthèse du hasard et des opérations déductives (compositions probabilistes)

Ce document, qui hiérarchisait et planifiait les activités d’apprentissage, prenait donc ses distances avec les fondements pédagogiques des manuels de T. Varga (VARGA, 1976, p. 6) qui, pour les enseignants aussi, organisait l’approche de l’aléatoire selon les étapes suivantes : « Le lecteur sera introduit par dans les domaines de la combinatoire, des probabilités simples, des probabilités conditionnelles et de la statistique descriptive simple. » Le document cité plus haut avançait que, même si le Professeur VARGA était convaincu à juste titre du rôle à donner à l’apprentissage de l’incertitude, à tous les niveaux de l’école élémentaire, dans les faits, la programmation de son projet était conçue « sur la base d’un découpage qui est strictement mathématique ; c’est à dire [selon] la succession des activités [qui] répond à un ordre qui est propre aux mathématiques (la combinatoire d’abord, le modèle mathématique d’analyse d’une situation ensuite, puis les statistiques qui préparent les activités de simulation.) »²⁴.

Pourtant sur le fond, les deux auteurs semblent s’accorder ; voilà ce qu’avance le Professeur VARGA, dans un autre ouvrage intitulé Hasard ou stratégie, (1976), déclarait à propos des faits rencontrés par les élèves (p. 186) :

‘« L’intelligence des faits déborde largement la simple constatation de similitudes entre diverses situations. En théorie des probabilités, cette phase ne pourra être atteinte que beaucoup plus tard, le domaine étudié étant beaucoup plus complexe. Même l’affirmation la plus sensée peut se révéler brusquement fausse, alors qu’une autre proposition, découlant d’une faute de jugement, peut se trouver confirmée [...]. On ne peut même pas être sûr de ce qui se produira dans la majorité des cas, et l’on doit toujours ajouter “très probablement”. Tout au plus, peut-on acquérir ou provoquer une certitude croissante, mais jamais une certitude absolue. C’est l’un des attraits de la théorie des probabilités, que de pouvoir accroître sans cesse cette certitude. Lorsque l’on soumet à de très jeunes enfants les premières épreuves aléatoires, en leur montrant les divers résultats possibles, ils pensent être à même de prédire le résultat. Les enfants plus grands, eux, diront : “on ne peut rien prédire du tout”. C’est un peu plus tard encore qu’ils découvriront que finalement il y a quand même quelque chose à dire. Du chaos apparent, ils dégageront des lois. Et ces expériences présentent pour eux un réel attrait. Des enfants de dix ans ne sont pas encore mûrs pour concevoir le calcul des probabilités comme une théorie déductive ; ils en sont mêmes très loin. Mais après quelques expériences, ils en comprendront souvent mieux intuitivement les lois que bien des adultes d’aujourd’hui. »’

Il semble poindre une convergence à propos des étapes d’appropriation de l’incertitude par les élèves entre les deux auteurs. La différence se situerait plutôt du côté de la présentation des faits d’incertitude : devons-nous attendre l’âge des possibilités d’acquisition par l’élève ou devons-nous les devancer au risque d’inciter les élèves, par manque de bagage mathématique, au recours aux explications magiques ! Cette perplexité fut exposée à l’issue de notre présentation de Bordeaux (2009), en toute connaissance des expériences conduites par des stagiaires de l’IUFM de Grenoble par exemple (cf. annexe 3.2) ; cette remarque fut d’ailleurs soutenue lors du débat qui suivit, par Guy Brousseau. Elle est aussi évoquée au fil de l’ouvrage de Benoît Rittaud, Les mystères du hasard (RITTAUD, 2008) qui explore le double paradoxe adressé aux élèves dans l’appropriation du concept de “hasard” :

Premièrement :

• Si l’on accepte l’existence du hasard, on valide les recherches sur les probabilités et du coup, on favorise la recherche actuelle et l’apport de réponses (partielles certes, dans l’idée de la connaissance pure) mais réelles dans la vie pratique. Et par contre, on repousse l’idée de la science pouvant aller encore plus loin dans l’explication du monde.
• Si l’on refuse l’existence du hasard, on favorise l’idée d’explication scientifique du monde, mais en contrepartie, on se prive d’outils d’approximation des résultats, souvent fort utiles sur le plan pratique.

Deuxièmement :

• Faire comprendre que le hasard, n’a rien du ressort de la magie, c’est faire en sorte que pour les élèves, ils en tirent l’idée que bien qu’imprévisibles, les événements suivent tout de même certaines régularités (loi des grands nombres).
• Mais dans ce cas, comment faire alors comprendre aux élèves que chaque événement est indépendant de l’historique des événements précédents ?

Pour notre part, en accord avec les auteurs précédents et en se reportant au dernier tableau, nous aimerions centrer la poursuite de ce travail sur la ligne intermédiaire qui le constitue (et qui correspond aux élèves ciblés par cette recherche) ; reportons-là ci-après :

Tableau 100 : Ligne centrale de la recherche envisagée

	Opérations logiques	Idée de hasard et de probabilité
Deuxième période (8/11 ans)	Construction de groupements opératoires d’ordre logique (niveau des opérations concrètes)	Différenciation et antithèse entre opérations (domaine du déductible) et hasard (domaine de l’“incomposable” et de l’irréversible)

La recherche pourrait donc s’illustrer de la manière suivante :

• proposer aux élèves des situations qui mêleraient soit des aspects “réguliers”, soit des aspects “aléatoires” (dans la prise en compte de la situation, des données, des variables, des registres sémiotiques, des indices statistiques utilisés, dans la communication des résultats, etc.),
• et d’en éprouver alors les pistes d’analyse entourant la prise de décision des élèves, c'est-à-dire rejoindre l’ouverture A4 signalée plus avant. Étudier comment les élèves se positionnent lorsqu’ils sont mis en présence de la résolution mathématique d’une situation. Sur quels critères, différencient-ils les situations où les mathématiques  :
• • leur donnent l’assurance d’obtenir un résultat (un résultat sûr et précis),
  • leur permettent d’avancer qu’aucun résultat n’est envisageable (résultat impossible),
  • ou leur semblent impuissantes (résultat incertain).

Sur quoi alors se fonderait la décision des élèves ? Tout d’abord, quelle serait la référence mathématique retenue par les élèves :

• leur propre savoir (se traduisant en leur capacité en cours, à résoudre mathématiquement le problème proposé),
• ou l’intuition (que les mathématiques peuvent opérer sans qu’eux-mêmes n’aient encore les capacités requises pour le faire) ?

Que représenterait ensuite pour eux l’idée d’apporter une réponse mathématique :

• est-ce une réponse précise, unique ?
• ou un ensemble de réponses, cadré par ses limites ?

Que serait l’élaboration par l’enseignant de situations dites fondamentales dans la terminologie de Brousseau pour installer les bases d’une didactique de la statistique ?

Pour les élèves, comment percevraient-ils les aspects réguliers ou aléatoires des situations à traiter ?